

How to Lie With Statistics
This is not the book that professors will pick up when they start teaching any course on statistics. Not at IITs, not at IIMs, not elsewhere. But they may well require students to read this book as a pre-requisite before enrolling for a course on statistics.
This is an excellent book to get you started on how to spot deceptions and dissembling via numbers and statistics, even if it is half a century old. Like wine, the book has aged and even got better with time. Short, readable, humorous, covers a variety of 'lies' spoken in the language of statistics, and still reads relevant five decades after it was first written. It won't educate you on statistics per se, on such terms as the bell curve, standard error, sampling error, confidence intervals, etc... but that is not the purpose of the book. Plenty of books in the market on these topics.
While Mark Twain (Wikipedia link) and Benjamin Disraeli (Wikipedia link) are both credited with having used and popularized the phrase, "There are three kinds of lies: lies, damned lies, and statistics" (Wikipedia page on "Lies, Damned Lies, and Statistics"), it is somewhat surprising that the first, or at least the first popular, book on the topic of using statistics to lie or confuse, appeared only in 1954.
How to Lie With Statistics
People lie with statistics. Some are smart enough to know how statistics and numbers can be employed to manipulate and to make these numbers appear to say whatever these people want them to say. Some make statistics lie through sheer hapenstance; there is nothing sinister or malafide in their actions. It just happens that way. Some are too clueless to really do anything with numbers, or to know what they mean.
This book has seen many successors, especially when it comes to the book's name, like How to Lie with Maps (2nd Edition)
The fact is that despite its mathematical base, statistics is as much an art as it is a science. A great many manipulations and even distortions are possible within the bounds of propriety. Often the statistician must choose among methods, a subjective process, and find the one that he will use to represent the facts. In commercial practice, is about as unlikely to select an unfavorable method as a copywriter is to call his sponsor's product flimsy and cheap when he might as well say light and economical. [page 120]
As Henry G. Felsen, a humorist and no medical authority, pointed out quite a while ago, proper treatment will cure a cold in seven days, but left to itself a cold will hang on for a week.There is a part of the human brain, and indeed heart also, that is so eager for the 'truth', in whatever context, in whatever form, that we look at numbers with a reassuring feeling - numbers convey accuracy, preciseness, and authority, which in turn leads us to accept them as being truthful. Words can be used to lie, numbers cannot - so goes the seductiveness of numbers.
The secret language of statistics, so appealing in a fact-minded culture, is employed to sensationalize, inflate,confuse, and oversimplify. ... But without writers who use the words with honesty and understanding and readers who know what they mean, the result can only be semantic nonsense. [page 8]
If your sample is large enough and selected properly, it will represent the whole well enough for most purposes. If it is not, it may be far less accurate than an intelligent guess and have nothing to recommend it but a spurious air of scientific precision. [page 13]
The basic sample is the kind called "random." It is selected by pure chance from the "universe," a word by which the statistician means the whole of which the sample is a part. ... The test of the random sample is this: Does every name or thing in the whole group have an equal chance to be in the sample? [page 20, 21]But, this kind of a 'pure' random sample is very difficult and very expensive to get. After all, if you were to try and obtain such a 1% random sample of the Indian population, you would end up with 10 million people, would have to travel the length and breadth of the country, across 626 districts, spread across 28 states and 7 union territories, cover an area of more than 3 million square kilometers, selected from over 1.15 billion people. That is one hundred and fifteen crore people. Or if you want to look at only the electorate, that would be some 715 million people - 715 followed by six zeros: 715000000. The summary of this is that obtaining a truly random, and representative sample in this case is very, very difficult, and the exercise best left to those educated and trained in this art and science.
Difficult and expensive - wouldn't you agree?
A more economical substitute, which is almost universally used in such fields as opinion polling and market research, is called stratified random sampling. [page 21]
No conclusion that "sixty seven per cent of the American people are against" something or other should be read without the lingering question, Sixty-seven per cent of which American people? [page 22]Does it, should it, come as a distressing surprise then that our media-persons gleefully parrot out statistics with such authority that you would be forgiven for thinking they actually knew what they were talking about? The results of a survey, for example, where people SMS their choice in, are treated with sacrosanct reverence, and through the magic of determined repeating acquire the halo of truth.
Never mind the issues with the framing of the question, where the questions are framed in such a way as to incite one particular response over another, the bias in the sample (only those who watch the channel AND have a cell phone), the size of the responses, whether one person is restricted to only one vote, and more. How many times have you seen news channels and newspapers that run polls announce to their viewers and readers that such polls are unscientific and their results usually irrelevant and have no more educational value than a used roll of toilet paper? You would not believe so, going by the serious debate that is conducted solely on the basis of such polls.
Or take the example of the recent advertisements that tout the health benefits of washing hands with one brand of soap. Double-blind tests... has anyone involved with the campaign ever heard of the term? Or does style have to massacre substance? Evidently so, if you see the spate of advertisements that follow this pattern. How many people? Could anything else have affected the result? Was there a control group? How was the selection of the children done? And so on...
So when you see an average-pay figure, first ask: Average of what? Who's included? The United States Steel Corporation once said that its employees' average weekly earnings went up 107 per cent between 1940 and 1948. So they did-but some of the punch goes out of the magnificent increase when you note that the 1940 figure includes a much larger number of partially employed people. If you work half-time one year and full-time the next, your earnings will double, but that doesn't indicate anything at all about your wage rate. [page 35]If you pay an autorickshaw 20 rupees to take you from MG Road to Museum Road in Bangalore, and if that ride takes 5 minutes, would you extrapolate this (5 minutes, 12 times an hour, 10 hours a day, 365 days a year) to claim that the autorickshaw driver's annual earnings are close to nine lakh rupees? No. You wouldn't. You shouldn't.
Users report 23% fewer cavities with Doakes' tooth paste, the big type says. You could do with twenty-three per cent fewer aches, so you read on. These results, you find, come from a reassuringly "independent" laboratory, and the account is certified by a certified public accountant. What more do you want?
Yet if you are not outstandingly gullible or optimistic, you will recall from experience that one tooth paste is seldom much better than any other. Then how can the Doakes people report such results? Can they get away with telling lies, and in such big type at that? No, and they don't have to. There are easier ways and more effective ones.
The principal joker in this one is the inadequate sample - statistically inadequate, that is; for Doakes' purpose it is just right. That test group of users, you discover by reading the small type, consisted of just a dozen persons.
...
Sooner or later, by the operation of chance, a test group is going to show a big improvement worthy of a headline and perhaps a whole advertising campaign.
[pages 37, 38]
It is all too reminiscent of an old definition of the lecture method of classroom instruction: a process by which the contents of the textbook of the instructor are transferred to the notebook of the student without passing through the heads of either party. [page 47]
So if I were to tell you that given an unbiased coin I have a way by which to get heads four times out of five tosses, would you believe me? Likely not. Yet if I were to advertise a similar statistic in a marketing campaign for a children's health drink or an anti-septic soap, not many would question it. If I were to now tell you that I did this test of tossing a coin five times twice, and on the second test when I got four heads, I decided to take the results of this test, would it make any difference? Not likely, given that you have probably already decided that I am either a complete fake or a dishonest advertiser (tautologies notwithstanding).
Intelligence tests are the fetish in the USA, and it's only a matter of time before they become an obsession with our schools in India too. Chapter 4, "Much Ado About Practically Nothing", introduces us to the probable error and the standard error, using the example of an IQ test.
Just to clear the air, let's note first of all that whatever an intelligence test measures it is not quite the same thing as we usually mean by intelligence. It neglects such important things as leadership and creative imagination.Chapter 5, "The Gee-Whiz Graph", briefly gets into the area of lying with graphs. By using a scale that does not start at zero, or a line graph that is truncated to show only a small window of the actual graph, or by means of a broken graph, and more. See these examples below that I (re)created from the book below.
It takes no account of social judgment or musical or artistic or other aptitudes, to say nothing of such personality matters as diligence and emotional balance. On top of that, the tests most often given in schools are the quick-and-cheap group kind that depend a good deal upon reading facility; bright or not, the poor reader hasn't a chance. [page 54]
These are all fascinating examples, and if you want to learn more, Edward Tufte's books talk about chart junk in a great more detail. The Visual Display of Quantitative Information, 2nd edition
If annual sales for a company increased from 50 (million, billion, lakhs, crores - whatever) in 2001 to 54.4 in 2005, this chart does the best job of honestly displaying that information:
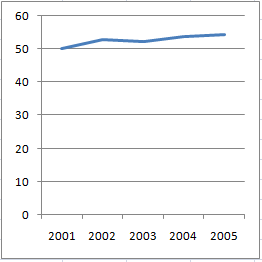
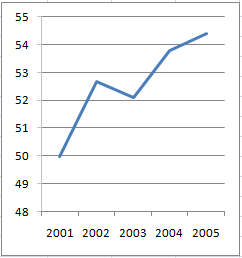
If you want to make the chart all jazzed up, or to simply obfuscate information, one obvious way to do that is by starting the vertical scale not at zero, but at a higher number like 48 or so, so that the increase now looks a lot more dramatic than before.
A second way is by simply removing the scale, so that the user has no way of finding out anything meaningful from the chart:
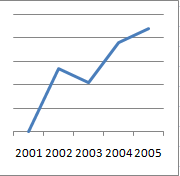
These are at two more ways in which to destroy any information that the chart could give the user.
A third way is by using a fake 3D effect for the chart, and to use useless ornamentation on the chart like conical bars, which make it next to impossible to perform meaningful comparisons across years:

You can also massacre the chart's utility by using a pie chart, which makes it close to impossible to compare individual values, made all the more difficult thanks to the 3D effect:

Chapter 6, "The One Dimensional Picture", is a continuation of the topic on lying with charts, and here the use of representing a single measure along a single dimension along two axes is described. For example, wage rate in two countries for a given year is an example of a single measure (wage rate) along one dimension (time). So it is best represented by a bar graph. But, to make it more 'interesting' or more 'visually' appealing, representations are used that distort the data. Here are two commonly used examples:


If the first circle represents 100, to represent 200, you double the size of the circle. Except, if you employ your knowledge of geometry, the area of the bigger cirlce is now four times (pie times r-squared, so if the radius doubles, the area increases four times) that of the smaller one. But you are not plotting a value of 400 for the larger circle, are you?
Ditto for the triangle. To display a value twice the first value, if you draw a triangle with twice the base and twice the height, you have a triangle with four times the area of the first one.
What would be an honest chart?
The humble bar chart, shorn of adornments:

If you can't prove what you want to prove, demonstrate something else and pretend that they are the same thing. In the daze that follows the collision of statistics with the human mind, hardly anybody will notice the difference. [page 74]Chapter 8, "Post Hoc Rides Again", is on correlations and causality. The title of the chapter is taken from the Latin phrase, "Post hoc ergo propter hoc", which means "after this therefore because of this", which is an example of a logical fallacy. If "a" follows "b", did "b" cause "a"? Or to put it another way: if the newspaper is delivered everyday at 7am, and if you go to the toilet at 7:30am, then did the newspaper delivery cause you visit the loo? You would most likely argue not. But you cannot dispute there is a strong correlation, though causality would be disputed, and rightly so, unless there is something in the newspaper content, everyday, that causes 'movement'.
...
If you can buy a juicer that is twenty-six per cent more effective, why buy any other kind? ... just what does that figure mean? Twenty-six per cent more than what? When it was finally pinned down it was found to mean only that this juicer got out that much more juice than an old-fashioned hand reamer could. It had absolutely nothing to do with the data you would want before purchasing; this juicer might be the poorest on the market. [page 77]
...
There are often many ways of expressing any figure. You can, for instance, express exactly the same fact by calling it a one per cent return on sales, a fifteen per cent return on investment, a ten-million-dollar profit, an increase in profits of forty per cent (compared with 1935-39 average), Or a decrease of sixty per cent from last year. The method is to choose the one that sounds best for the purpose at hand and trust that few who read it will recognize how imperfectly it reflects the situation. [page 82]
...
It is an interesting fact that the death rate or number of deaths often is a better measure of the incidence of an ailment than direct incidence figures-simply because the quality of reporting and record-keeping is so much higher on fatalities. [page 84]
Chapter 9, "How to Statisticulate" could have come straight from an Asterix comic book.
Misinforming people by the use of statistical material might be called statistical manipulation; in a word (though not a very good one), statisticulation. [page 100, bold emphasis mine]One lesson I remember being taught in math class in school, and I cannot in any honesty claim to have either learned the lesson precisely as the teacher intended to teach it or to have followed that advice as dilligently as I should have, was about precision and decimal places when doing multiplication.
For a spurious air of precision that will lend all kinds of weight to the most disreputable statistic, consider the decimal. Ask a hundred citizens how many hours they slept last night. Come out with a total of, say, 783.1. Any such data are far from precise to begin with. Most people will miss their guess by fifteen minutes or morc, and there is no assurance that the errors will balance out.But this obsession with precision can look silly at times, and make one appear awfully uneducated at other times.
... announce that people sleep an average of 7.831 hours a night. You will sound as if you knew precisely what you were talking about. If you had been so foolish as to declare only that people sleep 7.8 (or "almost 8"') hours a night, there would have been nothing striking about it. It would have sounded like what it was, a poor approximation and no more instructive than almost anybody's guess. [pages 106, 107]
Take another example:
... when the president of a flower growers' association said, in a newspaper interview, that "flowers are 100 per cent cheaper than four months ago," he didn't mean that florists were now giving them away. But that's what he said. [page 109]This above is an example of using the wrong base for comparison. 100% of a number is equal to the number itself, right? So if flowers cost Rs 10 a dozen four months ago, and if indeed the prices are now 100% cheaper, then that would mean they cost Rs 10 less a dozen. Which means, to lead this argument to its logical but (almost) absurd conclusion, that flowers are being sold for free (not "sold freely", which means something else). That is not the case. What is happening is that flowers are being sold for Rs 5 a dozen. And the the person is doing is thinking that since 5 is 100% of 5, therefore flowers are 100% cheaper than four months ago. That is wrong. Flowers are 50% cheaper than four months ago, since the price decrease has been 5 rupees, and 5 is 50% of 10. There you go.
In her History of the Standard Oil Company, Ida M. Tarbell went even further. She said that "price cutting in the southwest ranged from 14 to 220 percent." That would call for seller paying buyer a considerable sum to haul the oily stuff away. [page 109]Another example of how this base effect can be used to one's advantage is this: supposing you earn one lakh rupees a year. You get a hike of ten thousand ruppes, so that your salary is now 1,10,000 rupees. Your company says you have got a 10% hike. Which is correct. You however say that your salary is now only 9% higher than your old salary. Which is also correct, in a way, if you calculate ten thousand rupees as a percentage of your NEW salary.
Another fertile field for being fooled lies in the confusion between percentage and percentage points. If your profits should climb from three per cent on investment one year to six per cent the next, you can make it sound quite modest by calling it a rise of three percentage points. With equal validity you can describe it as a one hundred per cent increase. [page 114, 115]
Percentiles are deceptive too. When you are told how Johnny stands compared to his classmates in algebra or some aptitude, the figure may be a percentile. It means his rank in each one hundred students. In a class of three hundred, for instance, the top three will be in the 99 percentile, the next three in the 98, and so on. The odd thing about percentiles is that a student with a 99-percentile rating is probably quite a bit superior to one standing at 90, while those at the 40 and 60 percentiles may be of almost equal achievement. This comes from the habit that so many characteristics have of clustering about their own average, forming the "normal" bell curve we mentioned in an early chapter. [page 115]
 Let's see this with an example. I used Excel to generate a pseudo-random distribution of 250 scores, with each score between 0 and 30. How exactly did I do this? Well.. by using the randbetween(0,1) function thirty times for each of the 250 rows, and then adding up the values for each row to get to the score. Plotting a histogram gave me a nice looking bell curve.
Let's see this with an example. I used Excel to generate a pseudo-random distribution of 250 scores, with each score between 0 and 30. How exactly did I do this? Well.. by using the randbetween(0,1) function thirty times for each of the 250 rows, and then adding up the values for each row to get to the score. Plotting a histogram gave me a nice looking bell curve.What are the scores of the students in the top 4 percentile, i.e. students in the 96th or better percentile? That would be the top 10 students (out of the class of 250 students). Their scores are 17, 16, 15, 15, 15, 15, 14, 14, 14, 14.
And what about the students in the middle? i.e. students between the 48th and 52nd percentiles? That would be the 10 students ranked 121 to 130. Their scores? 10, 10, 10, 10, 10, 10, 10, 10, 10, 10
QED.
Chapter 10 is the last one, and gives the reader five questions to ask when looking a statistic in the eye to try and discern the truth from the numbers, or to at least find out how phony and meaningless these numbers are:
Not all the statistical information that you may come upon can be tested with the sureness of chemical analysis or of what goes on in an assayer's laboratory. But you can prod the stuff with five simple questions, and by finding the answers avoid learning a remarkable lot that isn't so. [page 122]The five questions are:
Who Says So? How Does He Know? What's Missing? Did Somebody Change the Subject? Does it Make Sense?
- Darrell Huff - Wikipedia, the free encyclopedia
- WW Norton catalog page for the book
- Preview the book on Amazon.com
- More information on the book on Google Book Search
- How to Spot Statistical Jokers; by Darrell Huff, August 22, 1954, Sunday - Free Preview - The New York Times
While the longevity of How to Lie with Statistics must have come as a surprise to Huff, the seeds for its initial success were carefully planted. Remarkably, it was reviewed twice in The New York Times, a feat that would be almost impossible today. First, on January 4, 1954, Burton Crane gave it a column [4] and-a-half in “The Business Bookshelf”; then on January 16, it got another half column [30] in Charles Poore’s “Books of The Times.” Both reviews were highly positive, though not especially insightful. In August of 1954, Huff got to follow up in the Times with a more informative feature article [11] of his own, “How to Spot Statistical Jokers.” At the bottom of the first column, Huff added a footnote that says “Darrell Huff is a specialist in reading between statistical lines. He is the author of the book How to Lie with Statistics.” This does indeed seem to be how the world most remembers him today.
...
When one asks what may have led to the remarkable success of How to Lie with Statistics, it is natural to consider four likely sources: the title, the illustrations, the style and the intellectual content. In each case, from the perspective of fifty years, one finds more than might have originally met the eye.
- How to Lie With Statistics
- Innumeracy: Mathematical Illiteracy and Its Consequences
- A Mathematician Reads the Newspaper
- More Damned Lies and Statistics: How Numbers Confuse Public Issues
- Damned Lies and Statistics: Untangling Numbers from the Media, Politicians, and Activists
- 200% of Nothing : An Eye-Opening Tour through the Twists and Turns of Math Abuse and Innumeracy
- The Visual Display of Quantitative Information, 2nd edition
- Envisioning Information
- Information Dashboard Design: The Effective Visual Communication of Data
- How to Lie With Charts
- How to Lie with Maps
- Lies, Damned Lies, and Drug War Statistics: A Critical Analysis of Claims Made by the Office of National Drug Control Policy
- Lies, Damned Lies, and Science: How to Sort through the Noise around Global Warming, the Latest Health Claims, and Other Scientific Controversies
- That Woman : Lies, Damned Lies & Clintonisms